Transformation Examples

Example1: Transformation of UML/OCL model with Multiple inheritance into FoCaLiZe.


The following example shows a UML class diagram with multiple inheritances and OCL invariants. It consists of the class Person and its sub-classes Student, Teacher and Researcher. Then, the classes ResearcherStudent and ResearcherTeacher are created by means of multiple inheritances from the classes Student, Teacher and Researcher.
Note that the operation Person() is the class Person constructor, the operation equal() is a binary operation to decide whether two persons are equal, the attribute SSN shows the Social Security Number for both teachers and researchers and the type SPECIALITY is a UML enumeration class.
Photo de mon gite
The annotations attached to the classes Person, Teacher and Student are OCL invariants, which respectively specify:

The next FoCaLiZe code shows the transformation of the classes Person, Teacher, Researcher, ResearcherTeacher and ResercherStudent of the above figure:

open "basics";;
open "float_func" ;;
open "string_func";;


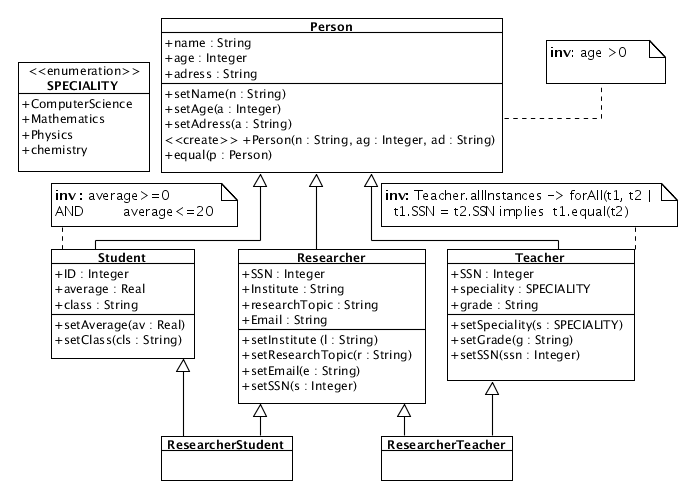
species Person =
signature name: Self -> string;
signature age: Self -> int;
signature adress: Self -> string;
signature setName : Self -> string -> Self;
signature setAge : Self -> int -> Self;
signature setAdress : Self -> string -> Self;
signature newPerson : string -> int -> string -> Self;
signature equal: Self -> Self -> bool;
(* invariant tarnsformation *)
property inv_1 : all e : Self, age(e) >=0x 0 ;
end;;


(* Transformation of enumeration SPECIALITY *)
type sPECIALITY = | ComputerScience | Mathematics | Physics | Chemistry ;;

species Researcher = inherit Person;
signature sSN: Self -> int;
signature institute: Self -> string;
signature researchTopic: Self -> string;
signature email: Self -> string;
signature setInstitute : Self -> string -> Self;
signature setResearchTopic : Self -> string -> Self;
signature setEmail : Self -> string -> Self;
signature new_Researcher :int -> string -> string -> string -> Self ;
end;;

(* species Teacher *)

species Teacher = inherit Person;
signature sSN: Self -> int;
signature speciality: Self -> sPECIALITY ;
signature grade: Self -> string;
signature setSpeciality : Self -> sPECIALITY -> Self;
signature setGrade : Self -> string -> Self;
signature new_Teacher :int -> sPECIALITY -> string -> Self ;

property inv_2 : all t1 t2: Self, equal(t1, t2) -> (sSN(t1) = sSN(t2)) ;
end;;

(* species Student *)
species Student = inherit Person;
signature iD: Self -> int;
signature average: Self -> float;
signature class: Self -> string;
signature setAverage : Self -> float -> Self;
signature setClass : Self -> string -> Self;
signature new_Student :int -> float -> string -> Self ;

property inv_3 : all e : Self, (average(e) >=f 0.0) /\ (average(e) <=f 20.0) ;

property prop_1 : all n : int, all f: float, all s : string,
(average(new_Student(n, f, s)) >=f 0.0) /\ (average(new_Student(n, f, s)) <=f 20.0) ;

property prop_2 : all e : Self, all f: float,
(average(setAverage(e, f)) >=f 0.0) /\ (average(setAverage(e, f)) <=f 20.0) ;

property prop_3 : all e : Self, all s : string,
(average(setClass(e, s)) >=f 0.0) /\ (average(setClass(e, s)) <=f 20.0) ;

(* Proof of the property inv_3 *)
proof of inv_3 =
<1>1 assume e : Self,
prove (average(e) >=f 0.0) /\ (average(e) <=f 20.0)
<2>1 prove (average(e) >=f 0.0)
by property prop_1, prop_2, prop_3
<2>2 prove (average(e) <=f 20.0)
by property prop_1, prop_2, prop_3
<2>3 qed by step <2>1, <2>2
<1>2 conclude ;
end;;
(* species ResearcherTeacher *)

species ResearcherTeacher = inherit Teacher, Researcher;
end;;
species ResearcherStudent = inherit Student, Researcher;
end;;


Example 2: Transformation of a real UML/OCL model with State Machines:


We present here the UML/OCL specification of a control system of a railway crossing a road.
This system consists of a controller, a traffic light and a barrier. For simplicity purposes, classes modeling trains and cars are not presented. The class diagram of the system is shown as follows:

Photo de mon gite
In the normal state, the light is green and the barrier is open. When the train arrives, the controller stops the traffic, turns the light to red and closes the barrier.
When the train has gone, the controller turns the light back to green and opens the barrier. The UML state machines describing this behavior are presented as follows:


Photo de mon gite


The next FoCaLiZe code shows the transformation of the classes Barrier, Light and Control: 


	


open "basics" ;;


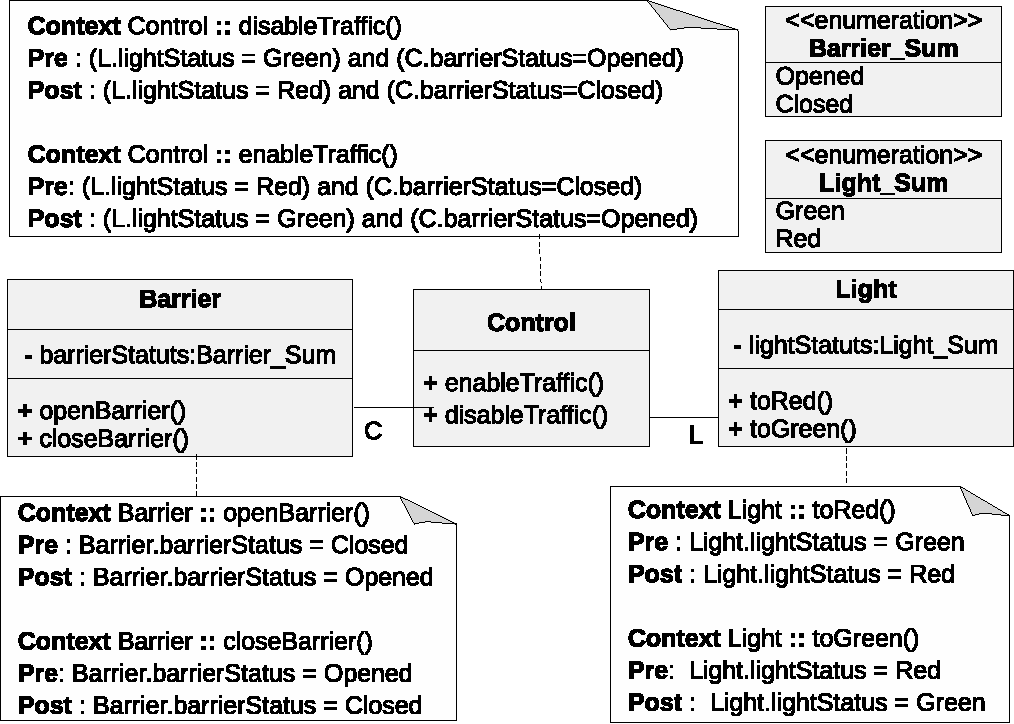
type barrier_Sum = | Opened | Closed ;;
type light_Sum = | Green | Red ;;

type control_Sum = | TrafficEnabled | TrafficDisabled ;;

(************************* The species Barrier transforms the class Barrier *)
species Barrier = 
 signature  get_barrierStatus : Self -> barrier_Sum;
 signature  openBarrier: Self -> Self;
 signature  closeBarrier: Self -> Self;
 signature  newBarrier: barrier_Sum -> Self;

 (* OCL constraints transformation *) 
 property prepost_openBarrier : all  b : Self,
 (get_barrierStatus(b)= Closed) -> (get_barrierStatus(openBarrier(b)) = Opened) ;

 property prepost_closeBarrier : all  b : Self,
 (get_barrierStatus(b)= Opened) -> (get_barrierStatus(closeBarrier(b)) = Closed) ; 


 (* Transformation of the state machine  of the class Barrier *)
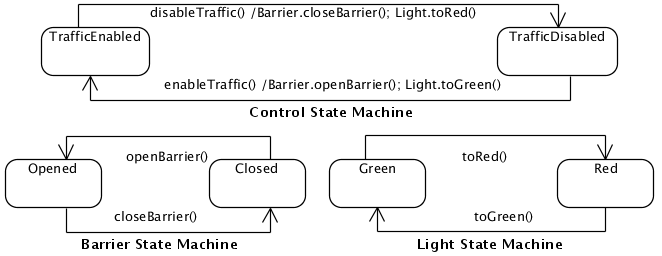
 let barrierTransitions  (b:Self):Self = match  (get_barrierStatus(b)) with
 | Closed -> openBarrier(b)
 | Opened -> closeBarrier(b);

 (* Theorems deducted from the state machine of the class Barrier *)

 property barrierTransition_Specification_1 : all b :Self,
  (get_barrierStatus(b)= Opened) ->  (get_barrierStatus(barrierTransitions(b)) = Closed) ;

 property barrierTransition_Specification_2 : all b :Self,
  (get_barrierStatus(b)= Closed) ->  (get_barrierStatus(barrierTransitions(b)) = Opened) ;
 end;;






(************************* The species Light transforms the class Light *)
species Light = 
 signature  get_lightStatus : Self -> light_Sum; 
 signature  toRed : Self -> Self;
 signature  toGreen : Self -> Self;
 signature  newLight: light_Sum -> Self;
 
 (* OCL constraints transformation *)
 
 property prepost_toGreen : all  l : Self,
 (get_lightStatus(l)= Red) -> (get_lightStatus(toGreen(l)) = Green);


 property prepost_toRed : all  l : Self,
 (get_lightStatus(l)= Green) -> (get_lightStatus(toRed(l)) = Red);


 (* Transformation of the state machine  of the class Light *)
  let lightTransitions(l:Self):Self =  match  (get_lightStatus(l)) with
  | Green -> toRed(l)
  | Red -> toGreen(l);
  
  
  (* Theorems deducted from the state machine of the class Light *)
  property lightTransition_Specification_1 : all l :Self,
  (get_lightStatus(l)= Green) ->  (get_lightStatus(lightTransitions(l)) = Red) ;

  property lightTransition_Specification_2 : all l :Self,
  (get_lightStatus(l)= Red) ->  (get_lightStatus(lightTransitions(l)) = Green) ;

 end;;






(************************* The species Control transforms the class Control *)
species Control (L is Light, B is Barrier)=

 signature enableTraffic : Self -> Self;
 signature disableTraffic : Self -> Self;
 signature get_Control_L : Self -> light_Sum;
 signature get_Control_B : Self -> barrier_Sum;
 signature  newBarrier: light_Sum -> barrier_Sum -> Self;
 signature get_ControlStatus : Self -> control_Sum;

 property prepost_disableTraffic : all  c : Self,
  ( ((get_Control_L(c)) = Green) /\
    ((get_Control_B(c))= Opened) ) -> 
  ( ((get_Control_L(disableTraffic(c)))= Red) /\
    ((get_Control_B(disableTraffic(c)))= Closed)  ) ;


 property prepost_enableTraffic : all  c : Self,
  ( ((get_Control_L(c))= Red) /\
    ((get_Control_B(c))= Closed) ) -> 
  ( (get_Control_L(enableTraffic(c)) = Green) /\
    ((get_Control_B(enableTraffic(c))) = Opened) );



 let controlTransitions  (c:Self):Self = match (get_ControlStatus(c))  with
  | TrafficEnabled ->   disableTraffic(c)
  | TrafficDisabled -> enableTraffic(c);


 property specif_controlTransitions_1 : all c :Self,
 (get_ControlStatus(c)= TrafficEnabled)  ->   
                       get_ControlStatus(controlTransitions(c))= TrafficDisabled ; 
  
 property specif_controlTransitions_2 : all c :Self,
    (get_ControlStatus(c)= TrafficDisabled) ->  
                       get_ControlStatus(controlTransitions(c)) = TrafficEnabled;


 end;;

  (**************************   IMPLEMENTATIONS  *****************************
   **************************                    *****************************
   **************************                    *****************************)

(* *** The species ConcreteBarrier *** *)
species ConcreteBarrier = inherit Barrier;
 representation = barrier_Sum;
 let newBarrier (b:barrier_Sum):Self = b ;

 let get_barrierStatus(b:Self):barrier_Sum = if (b = Opened) then Opened else Closed ;  

 let openBarrier(b:Self):Self = newBarrier(Opened) ;
 let closeBarrier(b:Self):Self = newBarrier(Closed) ;


  (* OCL constraints transformation *)

 proof of prepost_openBarrier = by definition of newBarrier, get_barrierStatus, openBarrier type    
 barrier_Sum;

 proof of prepost_closeBarrier = by definition of newBarrier, get_barrierStatus, closeBarrier type 
 barrier_Sum;

  

proof of barrierTransition_Specification_1 =
   <1>1 assume b : Self, 
        hypothesis h1 : (get_barrierStatus(b) = Opened), 
        prove (get_barrierStatus(b)= Opened) ->  (get_barrierStatus(barrierTransitions(b)) = Closed)

   <2>1 prove  (barrierTransitions(b)) = closeBarrier(b)
        by  type barrier_Sum hypothesis h1 definition of barrierTransitions
   <2>2 qed by hypothesis h1 step <2>1 property prepost_closeBarrier
   <1>2 conclude;



proof of barrierTransition_Specification_2 =
   <1>1 assume b : Self, 
        hypothesis h1 : (get_barrierStatus(b) = Closed), 
        prove (get_barrierStatus(b)= Closed) ->  (get_barrierStatus(barrierTransitions(b)) = Opened)

   <2>1 prove  (barrierTransitions(b)) = openBarrier(b)
        by  type barrier_Sum hypothesis h1 definition of barrierTransitions
   <2>2 qed by hypothesis h1 step <2>1 property prepost_openBarrier
   <1>2 conclude;

 end;;
 
 (* Creating a collection from ConcreteBarrier *)

 collection BarrierCollection = implement ConcreteBarrier ; end;;

 let bo = BarrierCollection!newBarrier(Closed);;

 let bc = BarrierCollection!openBarrier(bo);; 


  (* *** The species ConcreteLight *** *)
species ConcreteLight = inherit Light;
 representation = light_Sum;
 let newLight (l:light_Sum):Self = l ;

 let get_lightStatus(l:Self):light_Sum = if (l = Green) then Green else Red ;  

 let toRed(l:Self):Self = newLight(Red);

 let toGreen(l:Self):Self = newLight(Green) ;


  (* OCL constraints transformation *)

 proof of prepost_toRed = by definition of newLight, get_lightStatus, toRed type    
 light_Sum;

 proof of prepost_toGreen = by definition of newLight, get_lightStatus, toGreen type    
 light_Sum;


 proof of lightTransition_Specification_1 =
   <1>1 assume l : Self, 
        hypothesis h1 : (get_lightStatus(l) = Green), 
        prove (get_lightStatus(l)= Green) ->  (get_lightStatus(lightTransitions(l)) = Red)

   <2>1 prove  (lightTransitions(l)) = toRed(l)
        by  type light_Sum hypothesis h1 definition of lightTransitions
   <2>2 qed by hypothesis h1 step <2>1 property prepost_toRed
   <1>2 conclude;


 proof of lightTransition_Specification_2 =
   <1>1 assume l : Self, 
        hypothesis h1 : (get_lightStatus(l) = Red), 
        prove (get_lightStatus(l)= Red) ->  (get_lightStatus(lightTransitions(l)) = Green)

   <2>1 prove  (lightTransitions(l)) = toGreen(l)
        by  type light_Sum hypothesis h1 definition of lightTransitions
   <2>2 qed by hypothesis h1 step <2>1 property prepost_toGreen
   <1>2 conclude; 

 end ;;




  (* *** The species ConcreteLight *** *)
species ConcreteControl (L is Light, B is Barrier) = inherit Control(L, B);
 representation = (light_Sum * barrier_Sum);
 let newControl (l:light_Sum, b:barrier_Sum):Self = (l, b) ;

   
 let get_controlStatus(c:Self):control_Sum = match c with
  | (Green, Opened) ->   TrafficEnabled
  | (Red, Closed) -> TrafficDisabled
  | (Green, Closed) -> focalize_error ("ERROR")
  | (Red, Opened) ->   focalize_error ("ERROR");

 let enableTraffic(c:Self):Self = newControl(Green, Opened);

 let disableTraffic(c:Self):Self = newControl(Red, Closed);
 
 let get_Control_B(c:Self):barrier_Sum = snd(c);
 let get_Control_L(c:Self):light_Sum = fst(c); 


  (* ... *)

 end ;;